How to find poisson from some bottles using minimum lab mice
Here is an interesting but not straightforward question. Suppose there are 16 bottles of liquid. One of them is poisonous while others are normal water. You have some mice in hand and the task is to find poison in 24 hours using these mice. However, you can only tell whether a mouse drank poison after 24 hours. Now, how many mice do you have to use to find the poison?
It is not simple to most of people, if you don’t have the insight. Let me state the result here: If you have \(N\) bottles, you need \(\log_2 N\) mice at least. The result here is 4.
But why?
The explanation involves encoding. First, we number bottles from 0 to 15. For all those bottles, we can using binary encoding to name them. For example, the bottle numbered 0 should be encoded as \(0000\) and bottle numbered 14 should be encoded \(1110\). We let mouse number one drank bottles whose first digit is encoded as 1 and mouse number two drank bottles whose second digit is encoded as 1 and so on. Suppose after 24 hours, dead mice set is \(S\). Say \(S=\{1,3\}\). Then the poisonous bottle is encoded as \(1010\) which is bottle number 10 since it is the only bottle from which all mice in \(S\) drank.
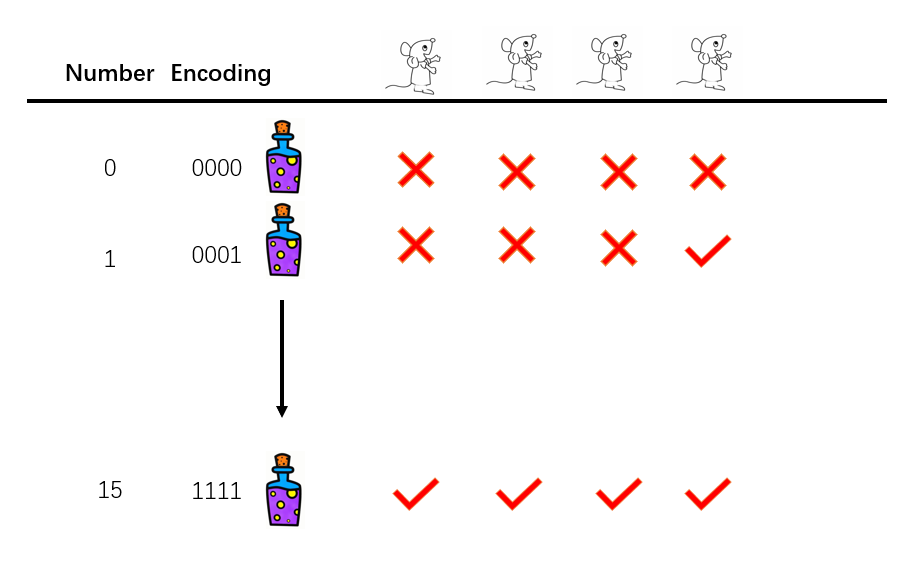
Now that we can use four mice to find the poison, how to know we cannot use just three of them to get the right answer? The simplest proof is to see this encoding is isomorphic. Since three mice can only have \(2^3\) different \(S\), \(S\) must be the same for some cases where the poison is in different bottles.
The proof can be done similarly if there are \(N\) bottles.