Approximate MAXMIN distance between K points in N dimension
When I was reading paper, namely The Relationship Between High-Dimensional Geometry and Adversarial Examples which generates a lot of points on the shell in high dimension, I thought of an interesting problem: what is the maximum of their minimum mutual distance. I googled and found this and this, while the first link asked exactly what I meant but got no ideal solution and the second one only solved a special case. However, though it might be intuitively easy to think about how the MAXMIN case looks like, it is not straightforward to get a unified solution. That motivates this blog.
I chose \(N\) from \(2\) to \(100\) with step \(5\) and \(K\) from \(10\) to \(200\) with step \(20\) and ran simulation for all these cases in Google Colab (code) and got this:
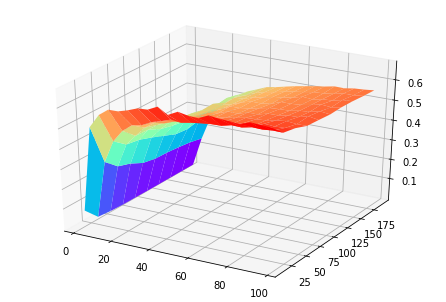
The illustration provides an insight which is also intuitively true. The MAXMIN increases as \(N\) (dimension) increases and decreases as \(K\) (number of points) increases. In addition, \(N\) has larger effect than $K$, and both seem to have convergent effects.
This blog is rather crude, so feel free to make improvements to my simulation.